For the past few years, I have been exploring the relationship between sentiment and plot shape in fiction. Earlier today I posted an R package titled “syuzhet” to github. The package is designed to extract sentiment and plot information from prose. Methods for text import, sentiment extraction, and plot arc modeling are described in the documentation and in the package vignette. What follows below is a blog-friendly version of a longer academic paper describing how I employed this package to study plot in a corpus of ~50,000 novels.
Still, all of these explanations of plot suffer from a significant problem: a lack of data. Each of these proposed taxonomies suffers from anecdotalism. Vonnegut draws the plot of Cinderella for us on his chalk board, and we can imagine a handful of similar plot shapes. He describes another plot and names it “man in hole,” and we can imagine a few similar stories. But our imaginations are limited.
This limitation led me to think hard about the problem of how to compare, mathematically and computationally, the shape of one story to another. Assuming I could use computers and some NLP magic to extract plot shape from narrative (see A Novel Method for Detecting Plot), it would still be impossible to compare one shape to another because of the simple fact that stories are not the same length. Vonnegut solved this problem by creating an x-axis that runs from B to E, that is, from beginning to end. What Vonnegut did not solve, however, was the real computational problem of text length.
It was tempting to consider simply breaking each book into ten or one-hundred equally sized pieces and then taking measurements of the mean emotional valence in each chunk.
Unfortunately, some of the books would have much larger chunks and with larger chunks would come the possibility of more and more diverse valence markers. What happens, in fact, is that larger chunks of text tend to have a preponderance of both positive and negative valence markers. The end result is that all the means end up very close to neutral on the y-axis of emotional valence. Indeed, books as a whole tend to have a mean valence close to zero on a scale of -1 to 1. (I tested this by calculating the mean valence for 3500 novels in my nineteenth century novels corpus and then plotting the results as a histogram. The distribution showed a clustering around zero with very few books on the extremes.)
So, I needed a way to deal with length. I needed a way to compare the shapes of the stories regardless of the length of the novels. Luckily, since coming to UNL, I’ve become acquainted with a physicist who is one of the team of scientists who recently discovered the Higgs Boson at CERN. Over coffee one afternoon, this physicist, Aaron Dominguez, helped me figure out how to travel through narrative time.
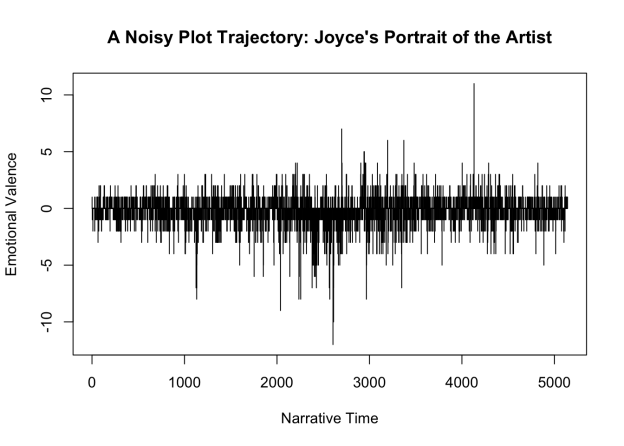
Aaron introduced me to a mathematical formula from signal processing called the Fourier transformation. The Fourier transformation provides a way of decomposing a time based signal and reconstituting it in the frequency domain. A complex signal (such as the one seen above in the first figure in this post) can be decomposed into series of symmetrical waves of varying frequencies. And one of the magical things about the Fourier equation is that these decomposed component sine waves can be added back together (summed) in order to reproduce the original wave form–this is called a backward or reverse transformation. Fourier provides a way of transforming the sentiment-based plot trajectories into an equivalent data form that is independent of the length of the trajectory from beginning to end. The frequency domain begins to solve the book length problem.